Les polygones réguliers.Un polygone est une forme constituée de plusieurs côtés (du grec polugônos: plusieurs coins). Les polygones réguliers sont des polygones spéciaux. D'abord ils sont plats (les mathématiciens disent "plans") et non croisés (aucun côté n'en coupe un autre), mais surtout: tous leurs côtés sont de la même longueur et tous leurs angles sont égaux.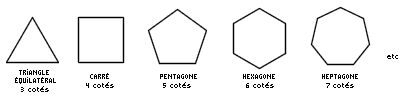
Remarquez que plus on rajoute de côtés à un polygone régulier, plus il ressemble à un cercle. Archimède voyait d'ailleurs le cercle comme un polygone régulier avec une infinité de côtés. Les polyèdres réguliers.Lorsqu'on assemble des polygones (en les collant côté contre côté) on obtient un polyèdre (disons une boite). Un polygone est plat, un polyèdre a une épaisseur, c'est un volume délimité par plusieurs faces (d'où son nom grec poluedros). Les polyèdres réguliers sont des polyèdres spéciaux: toutes leurs faces sont des polygones réguliers de même taille.Donc, pour faire un polyèdre régulier, c'est facile, on prend les polygones réguliers décrits ci-dessus (des triangles équilatéraux ou des carrés ou des pentagones, etc) et on les colle bord contre bord jusqu'à ce qu'on obtienne une belle boite (fermée et sans trou). Sauf que pour des raisons géométriques, ça ne marche qu'avec certains polygones, ceux de 3, 4 ou 5 côtés uniquement! C'est-à-dire avec des triangles équilatéraux, des carrés et des pentagones. Impossible de faire un volume fermé en n'utilisant que des hexagones de la même taille par exemple, il reste toujours des trous. Pire: même avec les formes qui marchent (triangles équilatéraux, carrés et des pentagones) impossible de faire tous les polyèdres réguliers qu'on veut. Si l'on s'en tient à des volumes convexes (une boite avec seulement des bosses et aucun creux) il n'y a en tout et pour tout que 5 possibilités: 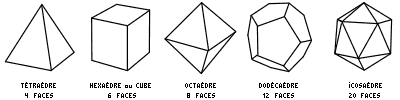
Cette limitation peut sembler bizarre mais prenez par exemple des carrés (tous de la même taille) et essayez de les assembler, bord contre bord, pour construire une boite (sans creux). Il n'y a qu'une seule et unique solution: un cube. Les grecs vénéraient ces 5 volumes qu'ils considéraient comme l'image même de la perfection. Platon notamment s'en est servi comme symboles philosophiques (5 polyèdres comme les 5 éléments, les 5 goûts, etc). D'où le nom qu'ils ont gardé de solides platoniciens. Pour tout savoir, mais vraiment tout, sur tous les polygones: LE site de Maurice STARCK. D'autres polyèdres (un peu) moins réguliers.Toujours en n'utilisant que des polygones réguliers (triangles équilatéraux, carrés, etc), si on décide ne pas se limiter seulement aux volumes convexes et qu'on accepte les solutions qui ont des creux (quoiqu'en pensaient les grecs) ça change tout. Au lieu des seuls 5 solides platoniciens on peut alors réaliser une infinité de polyèdres "presque" réguliers.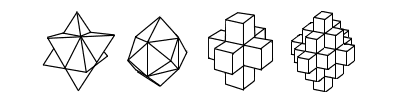
|